Tudósítás a jövőből

 

Tudják önök, hogy mit jelképez a szimbólum, ami egy kört és annak középpontját ábrázolja? A kör a végtelen és a középpontja annak kiindulópontja. A teremtés és a teremtő. Egységnyi átmérőjű kör egy pí kerületű kört teremt. Mi emberek ezt a pí-t nem vagyunk képesek megérteni és leírni. Nagyon régen az egyiptomiak néhány tizedest ismertek a számból, sokszor egyszerűen 3-nak számolták. A legtöbb ember 3,14-et ismer, de kiszámolták már több billió tizedes jegyig (cikk). Tudjuk, hogy egy végtelen és nem ismétlődő tizedes tört. Azt mondják rá, hogy egy transzcendens (nem levezethető) és irracionális szám (nem írható fel két szám hányadosaként).

3,14159265358979323846264338327950288419716939937510…
 

A teremtés végtelen, nem ismétlődő és nem vezethető le semmilyen matematikai egyenlettel - tehát irracionális és transzcendens. Kedves, hallgatóim, több az irracionális és transzcendens szám van a számegyenesen, mint a racionális. Összehasonlítatlanul több. Hiszünk a számokban, ez helyes, de csak a racionális számokat értjük, ez viszont kevés. Mily kis szelete a racionalitás a valóságnak!

 

Amikor a görögök felfedezték az irracionális számokat, akkor az aritmetika elvált a geometriától. A tartalom és a forma vált ketté. Pedig a kettő egymás nélkül nem létezhet! Meg is alkottuk az atombombát, de cseppet sem tudunk többet a teremtésről. Pitagorasz és tanítványai elakadtak az egységnyi oldalú négyzet átlójának hosszánál, ami gyök 2, egy irracionális szám!
 

 √2 az a szám, amit önmagával megszorozva 2-t eredményez, a dualitás számát. Irracionális!
 

 Pí az szám, ami a négyszögből kört csinál, a teremtés szimbólumát. Irracionális és transzcendens!
 

Nincs a világon elég tinta, hogy ezeket a számokat leírjuk!
 

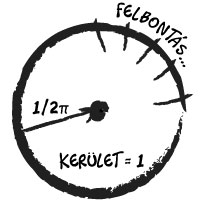
Jelen szemléletmódunk legnagyobb hiányossága, hogy nem tudunk megszerkeszteni egy egységnyi kerületű kört. Annak átmérője 1/pí kellene, legyen, és pí megismerhetetlen szám. Szintén nem tudunk egységnyi átlójú négyszöget rajzolni, mert annak élei 1/√2 kell, legyen. Tudunk(?) viszont egységnyi élű négyszöget és egységnyi átmérőjű kört konstruálni, mert van egységnyi egyenes szakaszunk (méter).

 

Ám óriási tévedés elhinni azt, hogy létezik egyenes! Egy épület homlokzata egyenesnek tűnik, de nem az! A föld görbületével párhuzamos, van íve! Párizsban őrzött méter etalonnak íve van. Einstein megmondta: a tér görbe! A háromszög szögeinek összege a valóságán soha nem 180 fok, csak közelíti a föld kis területén (lásd ábra).Az Euklideszi geometria alkalmatlan az univerzum leírására. Ez alapján a méterrúd két vége közti legrövidebb távolság (a fény útja) nem 1 méter, hanem annál rövidebb. Tehát belátható, hogy nem tudunk még egységnyi átmérőjű kört és egységnyi élű négyzetet sem szerkeszteni!

 

Következtetésem, hogy rossz egységet használunk. Egy egyszerű szemléletváltással mindezeket a hiányosságokat ki tudjuk küszöbölni. A négyzet és az egyenes nem fordul elő a természetben, mégis ezekből vezetünk le mindent, a kör ellenben velünk van szinte mindenhol. Javaslatom: ne a négyzet definiálja a kört, hanem a kör a négyzetet. Rajzoljunk egy kört, és nevezzük ezt egységnyi kerületűnek. (Biztos vagyok benne, hogy a tudomány segítségével találni fogunk olyan módszert, amivel a jelenlegihez hasonló módon definiálni tudjuk a méterkört, ám modernebb eljárásokkal, mint a kripton-86 gáz hullámhosszához való hasonlítás, ami reverse engineering.)

 

Nincs tehát egyenes!  Akkor lépjünk tovább, és vigyázzanak, mert csalok! Eddig semmi újdonságot nem mondtam (lásd nem-euklideszi geometria). Viszont ha nincs egyenes, el kell felejtenünk a számoknak egyenesen való ábrázolását, a számegyenest – ahol a racionális, irracionális és transzcendens számok keverednek!
 

Az új definíció szerint helyezzük a számokat egy körre.  A számkörön csak racionális számok vannak 1/x formában. Minden irracionális vagy transzcendens szám a körön kívülre vagy belülre esik. A pozitív és a negatív számok attól függnek, hogy milyen irányba járjuk be a kört. A 0 és a ∞ ugyanaz. A semmi és a minden találkozik. Ennél fogva a nullával való osztás nem értelmetlen, hanem végtelent eredményez. A számkörön annyi szám van, amennyire felosztjuk azt. Egy 64-bites eszköznél, bináris rendszer esetén ez 2⁶⁴ (=18 446 744 073 709 551 615), kvatranáris rendszerben 4⁶⁴ (3,4028236692093846346337460743177e+38). Azt mondjuk, a valóságot 64-es bitmélységgel közelítjük.

A valóságot nem akkor ismerjük meg maximálisan, ha 2^∞ felbontást alkalmazunk, hanem ha minél közelebb kerülünk a középhez, az egyetlen ponthoz. Miután az egységnyi átmérőjű kör középpontja 1/pi távolságra van annak minden pontjától, megállapíthatjuk, hogy minél pontosabban ismerjük a pi-t, annál közelebb jutunk a középhez és annál többet tudunk a minket körbevevő valóságról. Ezt nevezi az új tudomány így: transzcendens utazás a középhez.

A javaslat részleteinek kidolgozásán elkezdtük a munkát.